Elementy wykresu h-x

Wykres h-x został wynaleziony w 1923 roku przez Richarda Molliera i umożliwia obserwację oraz obliczanie przemian stanu skupienia, jakie zachodzą w wilgotnym powietrzu pod wpływem ogrzewania, nawilżania, osuszania lub chłodzenia. Zmiany stanu skupienia można przy tym obliczać bezpośrednio z wykresu w sposób graficzny.

Składniki i parametry:
Wykres h-x podaje wszystkie istotne parametry niezbędne dla opisania stanu powietrza:

Temperatura	= t	w °C
Wilgotność bezwzględna	= x	w g/kg
Wilgotność względna	= r.F.	w %
Entalpia właściwa	= h	w kJ(1+x)kg
Gęstość	= p	w (kg/m3)

Budowa
Wykres h-x jest przedstawiony w ukośnym układzie współrzędnych. Dzięki wyborowi ukośnego układu współrzędnych poprawia się dokładność odczytu danych w obszarze nienasyconym powietrza wilgotnego. Ukośny układ współrzędnych zaproponowany przez Molliera tworzy się poprzez obrót osi x zgodnie z ruchem wskazówek zegara do momentu, w którym izoterma t = 0°C w obszarze nienasyconym wilgotnego powietrza przebiega poziomo.
Linie stałej entalpii właściwej h przebiegają z lewej górnej strony do prawej dolnej strony wykresu. Linie stałej zawartości wody x przebiegają pionowo.

Oś pozioma, na której oznaczona jest zawartość wody, nie przebiega ze względów praktycznych przez początek układu współrzędnych. Jako drugą oś x można przyjąć wartości ciśnienia cząstkowego pary wodnej, gdyż jest ono zależne jedynie od zawartości wody x i od ciśnienia powietrza p. Na liniach ukośnych oznaczone są wartości entalpii właściwej h. Na wykresie podane są rodziny krzywych temperatury powietrza, gęstości wilgotnego powietrza i wilgotności względnej.
Za pomocą podziałki brzegowej można w łatwy sposób nakreślić na wykresie przemianę stanu skupienia, np. po nawilżeniu parą. Indeks 1+x oznacza, że entalpia wilgotnego powietrza składa się z entalpii suchego powietrza i entalpii wody. Linie stałej temperatury (izotermy) rosną łagodnie w obszarze powietrza nienasyconego o wartość entalpii pary wodnej. W punkcie nasycenia (wilgotność względna = 1) linie załamują się do dołu, gdyż powyżej punktu oznaczającego maksymalną zawartość pary wodnej woda może występować w powietrzu jedynie w postaci małych kropel (mgły). Po przejściu przez punkt nasycenia w obszar mgły izoterma odchyla się od izentalpy nieznacznie o wartość entalpii dodatkowej ilości wody.

W obszarze nienasyconego powietrza występują krzywe stałej wilgotności względnej, które powstają przez równy podział odpowiednich fragmentów izoterm między = 0 i = 1. Względna wilgotność zmniejsza się zawsze wraz ze wzrostem temperatury powietrza dla danej niezmiennej zawartości wody x.

Obliczenia przy użyciu wykresu h-x

Ogrzewanie przy stałej wilgotności bezwzględnej
Na ilustracji obok został pokazany proces ogrzewania masy powietrza bez zmiany ilości zawartej w niej pary wodnej.
Co można odczytać z tego procesu?
Ogrzewanie zaczyna się w temperaturze 11°C (punkt 1) i kończy się w temperaturze 25°C (punkt 2). Wilgotność bezwzględna x jest stała w czasie trwania całego procesu i wynosi 4 g/kg. Natomiast wilgotność względna zmienia się z 50% w temperaturze 11°C na 20% w temperaturze 25°C. Ponadto zmienia się entalpia h (1+x) z 21,4 kJ/kg na 35 kJ/kg, a w końcu także gęstość z 1,24 kg/m3 na 1,17 kg/m3.

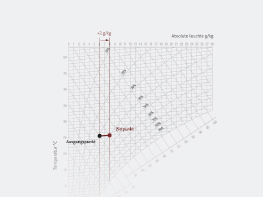
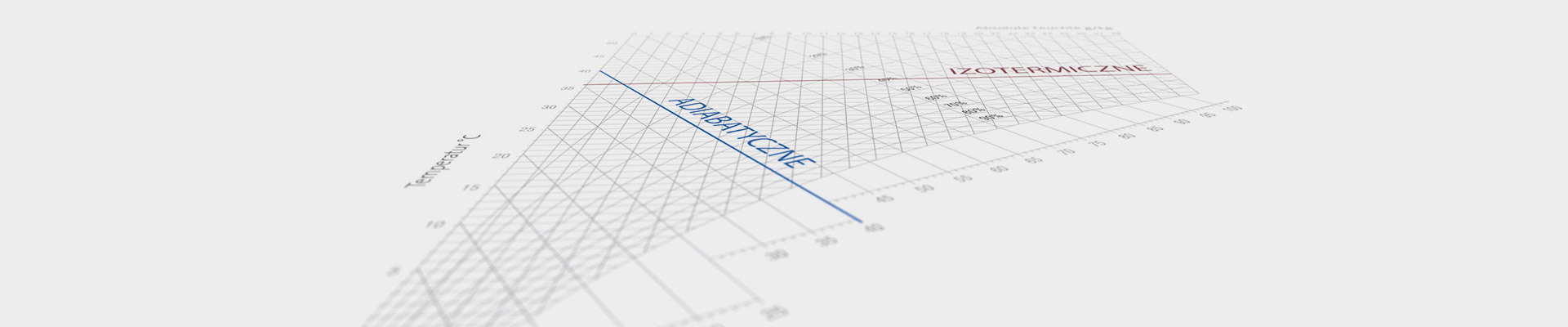
Rozpylanie lub odparowanie wody (nawilżanie adiabatyczne)
W procesie rozpylania i odparowania bez doprowadzenia ciepła z zewnątrz energia potrzebna do odparowania wody jest pobierania z otoczenia. Powietrze zatem ochładza się. Proces chłodzenia, przebiegający równolegle do adiabat, nosi nazwę chłodzenia adiabatycznego. Na wykresie h-x można dokładnie odczytać kierunek procesu chłodzenia podczas nawilżania korzystając z podziałki brzegowej ∆h/∆x.

Obliczanie zależności ∆h/∆x:

∆h	=	kJ/kg
∆x		kg H2O / kg suchego powietrza

Nawilżanie przy użyciu pary (nawilżanie izotermiczne)
Podczas nawilżania przy użyciu pary temperatura w procesie pozostaje zasadniczo stała, gdyż para wodna znajduje się na tym samym poziomie energetycznym co powietrze.

Obliczanie zależności ∆h/∆x:

∆h	=	kJ/kg
∆x		kg suchego powietrza